Matematika menjadi salah satu mata pelajaran yang harus dipelajari sejak duduk dibangku sekolah dasar, atau bahkan tingkat kanak-kanak. Matematika menjadi salah satu dasar mata pelajaran yang penting untuk dipahami dan dipelajari.
Hal ini memiliki tujuan untuk dapat membantu pola berpikir yang sistematis dan terstruktur. Sehingga dapat memudahkan kita dalam menjalankan kehidupan setelahnya. Dengan adanya matematika yang dipelajari sejak dini, akan memudahkan kita agar familiar dengan pola-pola matematika dan terkadang digunakan dalam kehidupan nyata.
Sehingga hal ini perlu untuk dipelajari dan dimanfaatkan dalam kehidupan sehari-hari. Dengan adanya pemahaman mengenai matematika, dapat membantu gaya hidup yang disiplin dan sesuai dengan rencana. Segala hal yang diperhitungkan dengan baik dan benar dapat membantu tujuan tercapai dengan mudah. Sama halnya dengan matematika yang membutuhkan ketelitian dan keuletan dalam berfikir dan menghitung.
Rumus Belah Ketupat
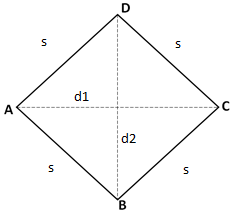
Salah satu rumus yang dipelajari dalam dunia matematika adalah rumus belah ketupat. Belah ketupat adalah bentuk model dari layang-layang. Belah ketupat memiliki 4 sisi yang sama panjang.
Dimana belah ketupat ini merupakan bangun 2 dimensi yang semua sisinya berukuran sama. Belah ketupat terdiri dari 2 segitiga sama kaki yang identik. Sehingga bentuknya dapat menyerupai segitiga yang saling berhadapan. Belah ketupat memiliki rumus yang sederhana, yaitu untuk mengetahui luasnya dan kelilingnya. Berikut merupakan rumus belah ketupat:
Luas belah ketupat = ½ x d1 x d2
Keterangan:
d1 : merupakan diagonal 1
d2: merupakan diagonal 2
Sedangkan untuk menghitung kelilingnya adalah dengan rumus:
Keliling belah ketupat = 4 x s
Keterangan:
S: merupakan panjang sisi dari belah ketupat.
Contoh Soal dan Pembahasannya

Untuk memudahkan pemahaman mengenai rumus belah ketupat yang sudah dibahas, akan lebih mudahnya jika anda memahami soal-soal yang menjelaskan mengenai belah ketupat. Hal ini akan lebih mempermudah anda dalam belajar mengenai belah ketupat. Berikut merupakan beberapa contoh soal dan pembahasan dari rumus belah ketupat.
- Tentukan luas belah ketupat, jika garis yang membentang di tengah belah ketupat adalah sebesar 12 cm dan 15 cm.
Jawaban:
Jika garis yang membentang ditengah adalah 12 cm dan 15 cm, maka bisa dianggap bahwa 12 cm adalah d1, dan 15 cm adalah d2. Sehingga luas bangun belah ketupat tersebut adalah
Luas belah ketupat = ½ x d1 x d2 = ½ x 12 x 15 = ½ x 180 = 90 cm2
- Andi membutuhkan gambar belah ketupat untuk mewarnai hiasan yang dia buat untuk kerajinan tangan. Andi membutuhkan sepuluh buah bangun belah ketupat dengan masing-masing sisinya adalah 15 cm. Jika diketahui hal tersebut, maka berapa keliling belah ketupat yang dimiliki oleh andi?
Jawaban:
Jika masing-masing sisinya adalah 15 cm, maka keliling belah ketupatnya adalah
Keliling belah ketupat = 4 x s = 4 x 15 = 60 cm.
- Tentukan luas belah ketupat, jika garis yang membentang di tengah belah ketupat adalah sebesar 20 cm dan 25 cm.
Jawaban:
Jika garis yang membentang ditengah adalah 20 cm dan 25 cm, maka bisa dianggap bahwa 20 cm adalah d1, dan 25 cm adalah d2. Sehingga luas bangun belah ketupat tersebut adalah
Luas belah ketupat = ½ x d1 x d2 = ½ x 20 x 25 = ½ x 500 = 250 cm2
- Vina membutuhkan gambar belah ketupat untuk melengkapi pekerjaan rumah (PR) yang diberikan oleh Ibu Guru di Sekolah. Masing-masing sisi dari belah ketupatnya adalah 20 cm. Jika diketahui hal tersebut, maka berapa keliling belah ketupat yang akan dibuat oleh vina?
Jawaban:
Jika masing-masing sisinya adalah 20 cm, maka keliling belah ketupatnya adalah
Keliling belah ketupat = 4 x s = 4 x 20 = 80 cm.
- Jika diketahui keliling belah ketupat adalah sebesar 200 cm, maka berapa masing-masing sisi yang dimiliki belah ketupat?
Keliling belah ketupat adalah 200 cm, maka sisinya adalah
Keliling belah ketupat = 4 x s
200 = 4 x s
s = 200 / 4
s = 50 cm
Jadi, masing-masing sisi yang dimiliki oleh belah ketupat tersebut adalah sebesar 50 cm.
- Jika diketahui luas dari sebuah belah ketupat adalah sebesar 1375 cm2, dan salah satu diagonalnya sebesar 50 cm. Maka berapa panjang sisi lain yang dimiliki oleh belah ketupat tersebut?
Jawaban:
Jika luas belah ketupat adalah 1375 cm2, dan salah satu sisinya adalah 50 cm. Maka salah satu sisi tersebut bisa dianggap d1, dan d1 adalah 50 cm. Untuk itu kita perlu mencari besar d2.
Sehingga besar d2 adalah sebagai berikut:
Luas belah ketupat = ½ x d1 x d2
1375 = ½ x 50 x d2
1375 = 25 x d2
d2 = 1375 / 25
d2 = 55 cm
sehingga, besar sisi lainnya dari belah ketupat tersebut adalah sebesar 55 cm.
- Jika diketahui keliling belah ketupat adalah sebesar 1000 cm, maka berapa masing-masing sisi yang dimiliki belah ketupat?
Keliling belah ketupat adalah 1000 cm, maka sisinya adalah
Keliling belah ketupat = 4 x s
1000 = 4 x s
s = 1000 / 4
s = 250 cm
Jadi, masing-masing sisi yang dimiliki oleh belah ketupat tersebut adalah sebesar 250 cm.
Dengan adanya informasi mengenai rumus belah ketupat dan dilengkapi dengan contoh soal dan pembahasannya, akan lebih mempermudah kita sebagai orang yang ingin belajar matematika terkait rumus belah ketupat. Hal ini menjadi suatu referensi yang menarik untuk dipelajari untuk menambah wawasan kita sebagai siswa.
Semakin banyak referensi yang dapat dipelajari, maka akan semakin banyak pula informasi, pengetahuan dan wawasan kita mengenai berbagai macam hal.
Belajar matematika akan menjadi lebih mudah dengan adanya berbagai referensi pembahasan dan rumus yang mudah dimengerti. Hal ini dapat mendorong semangat belajar masing-masing siswa agar lebih bersemangat dalam belajar. Sehingga tidak ada lagi kata malas, jika sedang atau akan belajar. Belajar tidak hanya tentang matematika, namun bisa juga hal lainnya. Semoga artikel ini bermanfaat untuk anda.
Sumber https://indoint.com/


0 comments:
Post a Comment